rmutil and fitdistrplus

Warning in .check.version(config): Your configuration is compatible with version 0.8 of the ProjectTemplate package.
  Please run ProjectTemplate::migrate.project() to migrate to the installed version 0.8.2.

So the fix I did last week to computegetparam() (to allow “y” as an argument to the distribution functions) does allow fitdist to work (sort of) with the rmutil distributions. However, there can still be failures in estimatation or SE calculation, because there are a number of other ways that the rmutil distributions work differntly from the base distribution functions. fitdistrplus expects that:

• If the distribution parameters are out of bounds, ddist and pdist will return NaN (rmutil throws an error)
• If x is outside the support of dist, ddist will return zero (rmutil throws an error)
• If x is less than the minumum supported value of dist, pdist will return zero (rmutil throws an error)
• If x is greater than the maxumum supported value of dist, pdist will return one (rmutil throws an error)
• If x is NA, ddist and pdist will return an NA (rmutil throws an error)

So I’m going to need to rewrite the distribution functions. Fortunately they are in pure R—see https://github.com/swihart/rmutil/blob/master/R/dist.r. However, the rewriting will be painful enough that I’ll want to be selective about the distributions I pick!

Note that I can change y to x; but I still need to make the fix in fitdistcens, so will still need my local copy of fitdistplus. And because it needs to call functions that are not revealed outside the package environment, it needs to be part of a complete package.

I did just find in the fitdistr documentation that, in addition to distributions in the stats package, fitdistr provides inbuilt support (including initial values) for “invgamma”, “llogis”, “invweibull”, “pareto1”, “pareto”, “lgamma”, “trgamma”, “invtrgamma” from the actuar package.

I made the change to fitdistcens, and it is now getting past the initialization phase. But it still gets hung up because of the errors returned by dggamma and pggamma`.

Here are the updated functions:

dggamma

function (x, s, m, f, log = FALSE) 
{
    if (any(m <= 0)) 
        return(NaN)
    if (any(s <= 0)) 
        return(NaN)
    if (any(f <= 0)) 
        return(NaN)
    y <- x
    tmp <- log(f) + (f - 1) * log(y) + dgamma(y^f, s, scale = (m/s)^f, 
        log = TRUE)
    if (!log) 
        tmp <- exp(tmp)
    tmp
}

pggamma

function (q, s, m, f) 
{
    if (any(m <= 0)) 
        return(NaN)
    if (any(s <= 0)) 
        return(NaN)
    if (any(f <= 0)) 
        return(NaN)
    pgamma(q^f, s, scale = (m/s)^f)
}

And here’s a fit:

temp <- filter(disperseLer, ID == "100_0", Distance > 4)
cens_data <- cens_dispersal_data(temp, 7)
p1 <- fitdistcens(cens_data, "ggamma", start = list(s = 1.7, m = 11, f = 2))
summary(p1)

Fitting of the distribution ' ggamma ' By maximum likelihood on censored data 
Parameters
   estimate Std. Error
s 2.2711322  4.5620815
m 2.1207476  2.8582386
f 0.9187322  0.9675258
Loglikelihood:  -102.3071   AIC:  210.6143   BIC:  216.7956 
Correlation matrix:
           s          m          f
s  1.0000000 -0.9928811 -0.9944067
m -0.9928811  1.0000000  0.9973951
f -0.9944067  0.9973951  1.0000000

plot(p1)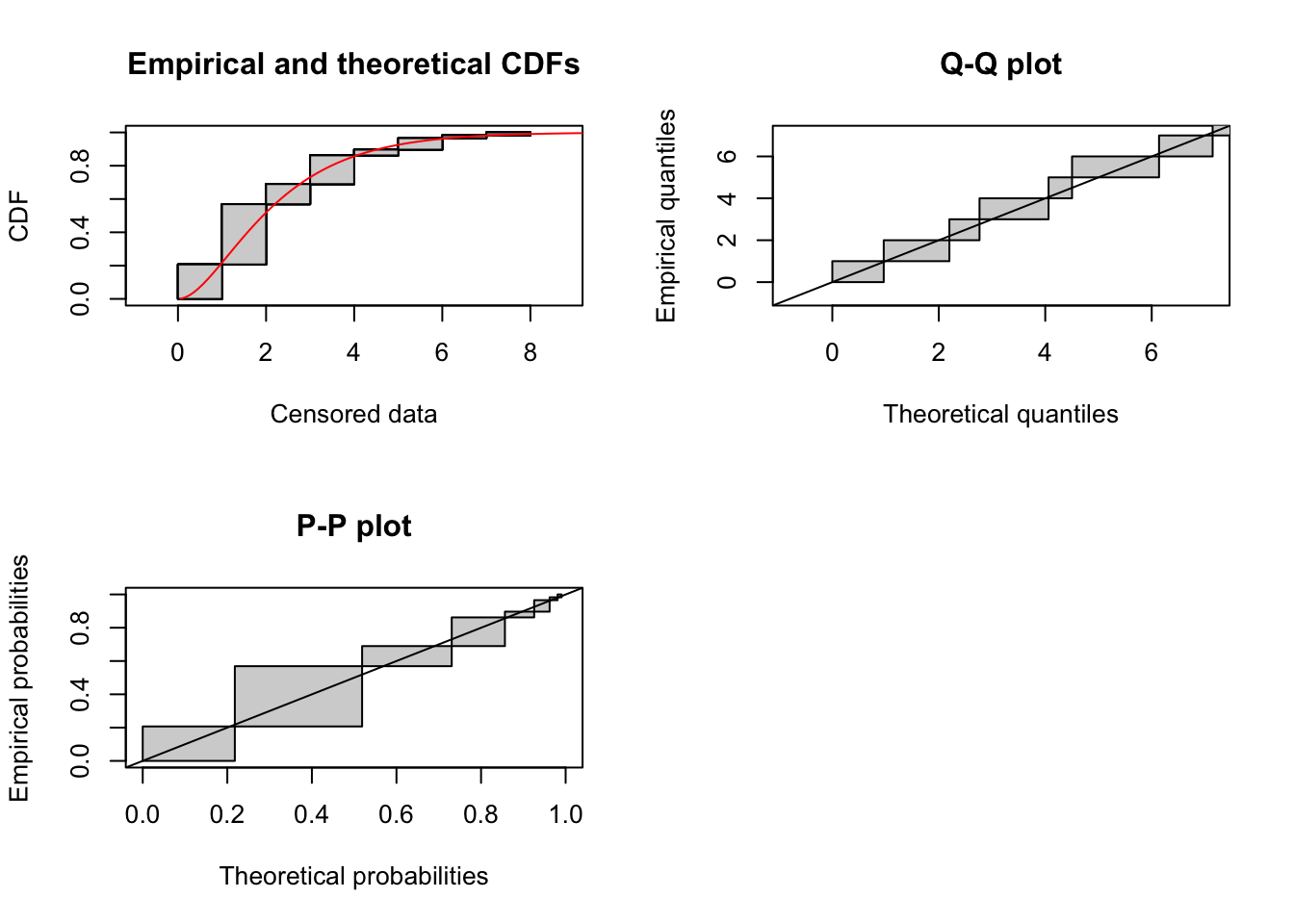 

The fit looks pretty good, but the correlation matrix suggests that it’s overparameterized. Also, not all start values for the parameters work!

Note that, if I want to use an offset different than 7, I’ll need to write truncated versions as well.