I’m not entirely satisfied with the prior post on the RIL dispersal kernels. So let me re-run some things and see what we understand.
First, we need to make sure that we are getting enough iterates in the fit:
controls <- list(maxit = 1000)We also clear out reps with not enough seeds (from 5/24/19):
n_min <- 10 # Set the minimum number of dispersing seeds
dispersing_seeds <- group_by(disperseRIL, ID) %>%
filter(Distance > 4) %>%
summarize(tot_seeds=sum(Seedlings))
good_reps <- filter(dispersing_seeds, tot_seeds >= n_min) %>%
pull(ID)
disperseRILgood <- filter(disperseRIL, ID %in% good_reps)So now fit all the reps.
RIL_list <- levels(disperseRILgood$RIL)
fiteach <- NULL
for (i in RIL_list) {
disperseRILi <- filter(disperseRILgood, RIL == i)
fiteachi <- cbind(RIL = i,
fiteach_disp_unt(disperseRILi,control=controls))
fiteach <- rbind(fiteach, fiteachi)
}<simpleError in optim(par = vstart, fn = fnobjcens, fix.arg = fix.arg, gr = gradient, rcens = rcens, lcens = lcens, icens = icens, ncens = ncens, ddistnam = ddistname, pdistnam = pdistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdistcens(cens_data_tble, model, start = start_params(cens_data_tble, :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobj, fix.arg = fix.arg, obs = data, gr = gradient, ddistnam = ddistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdist(cens_data_tble[, 2], model, start = start, ...) :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobjcens, fix.arg = fix.arg, gr = gradient, rcens = rcens, lcens = lcens, icens = icens, ncens = ncens, ddistnam = ddistname, pdistnam = pdistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdistcens(cens_data_tble, model, start = start, ...) :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobj, fix.arg = fix.arg, obs = data, gr = gradient, ddistnam = ddistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdist(cens_data_tble[, 2], model, start = start, ...) :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobj, fix.arg = fix.arg, obs = data, gr = gradient, ddistnam = ddistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdist(cens_data_tble[, 2], model, start = start, ...) :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobjcens, fix.arg = fix.arg, gr = gradient, rcens = rcens, lcens = lcens, icens = icens, ncens = ncens, ddistnam = ddistname, pdistnam = pdistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdistcens(cens_data_tble, model, start = start_params(cens_data_tble, :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobj, fix.arg = fix.arg, obs = data, gr = gradient, ddistnam = ddistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdist(cens_data_tble[, 2], model, start = start, ...) :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobjcens, fix.arg = fix.arg, gr = gradient, rcens = rcens, lcens = lcens, icens = icens, ncens = ncens, ddistnam = ddistname, pdistnam = pdistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdistcens(cens_data_tble, model, start = start, ...) :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobj, fix.arg = fix.arg, obs = data, gr = gradient, ddistnam = ddistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdist(cens_data_tble[, 2], model, start = start, ...) :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobj, fix.arg = fix.arg, obs = data, gr = gradient, ddistnam = ddistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [2]>
Error in fitdist(cens_data_tble[, 2], model, start = start, ...) :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobjcens, fix.arg = fix.arg, gr = gradient, rcens = rcens, lcens = lcens, icens = icens, ncens = ncens, ddistnam = ddistname, pdistnam = pdistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): non-finite finite-difference value [1]>
Error in fitdistcens(cens_data_tble, model, start = start_params(cens_data_tble, :
the function mle failed to estimate the parameters,
with the error code 100
<simpleError in optim(par = vstart, fn = fnobjcens, fix.arg = fix.arg, gr = gradient, rcens = rcens, lcens = lcens, icens = icens, ncens = ncens, ddistnam = ddistname, pdistnam = pdistname, hessian = TRUE, method = meth, lower = lower, upper = upper, ...): function cannot be evaluated at initial parameters>
Error in fitdistcens(cens_data_tble, model, start = start, ...) :
the function mle failed to estimate the parameters,
with the error code 100Now lets calculate the delta-AIC within each dataset:
result <- group_by(fiteach, ID) %>% mutate(delta_AIC = AIC - min(AIC))
ggplot(result, aes(x=delta_AIC, group = model)) + geom_histogram() +
facet_wrap(~model, scales = "free") `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.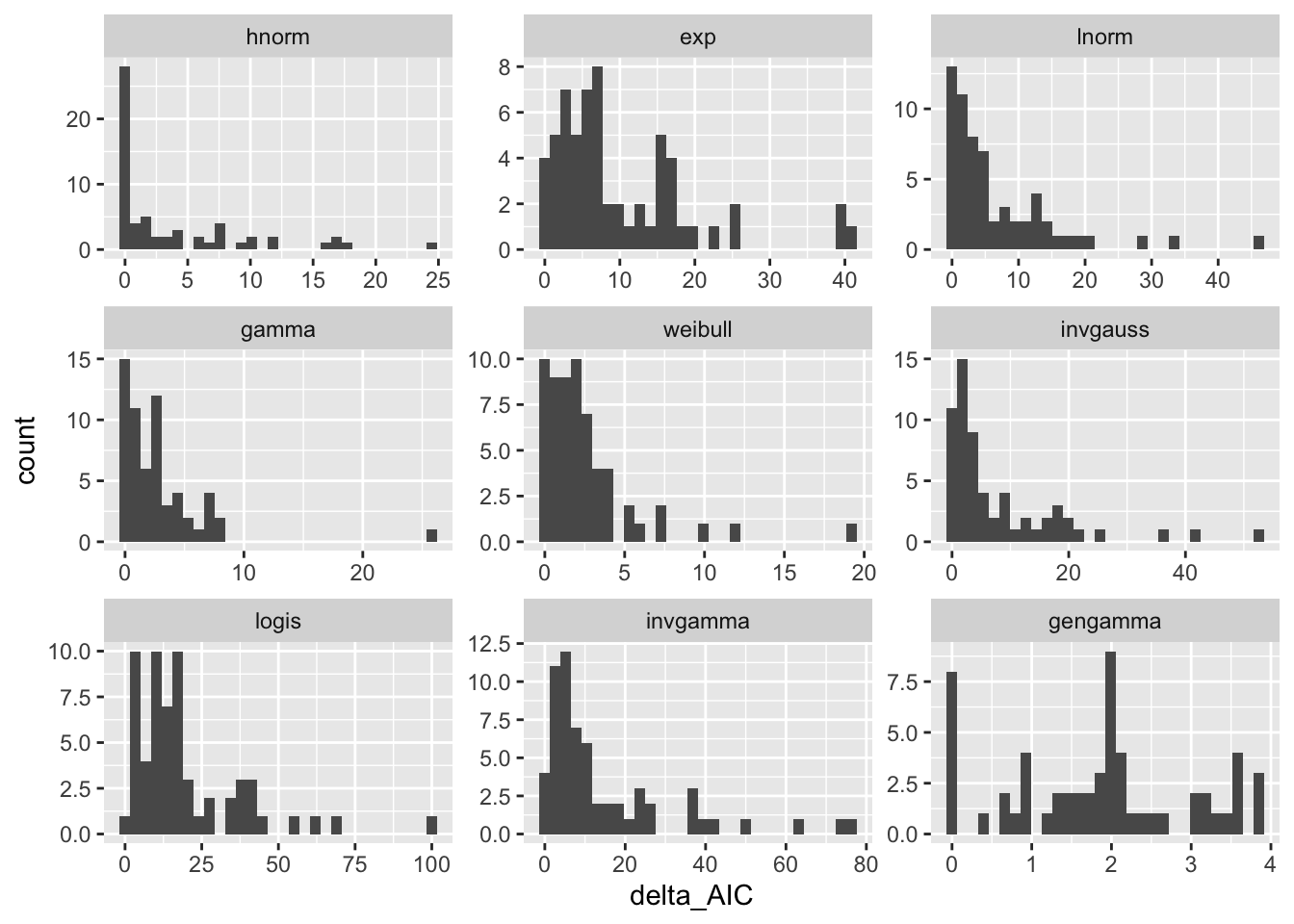
Once again, we confirm that the generalized gamma is the only model that always has a low \(\Delta\)-AIC.
Let’s look at the fitted kernels:
fiteachgg <- filter(fiteach, model == "gengamma")
p <- ggplot(data = data.frame(x = c(0, 20)), mapping = aes(x = x))
for (i in 1:nrow(fiteachgg)) {
pvec <- as.numeric(fiteachgg[i, 5:7])
plist <- list(mu = pvec[1], sigma = pvec[2], Q= pvec[3])
p <- p + stat_function(fun = dgengamma, args = plist, color = fiteachgg$RIL[i])
}
p + xlab("Distance (cm)") + ylab("Probability density")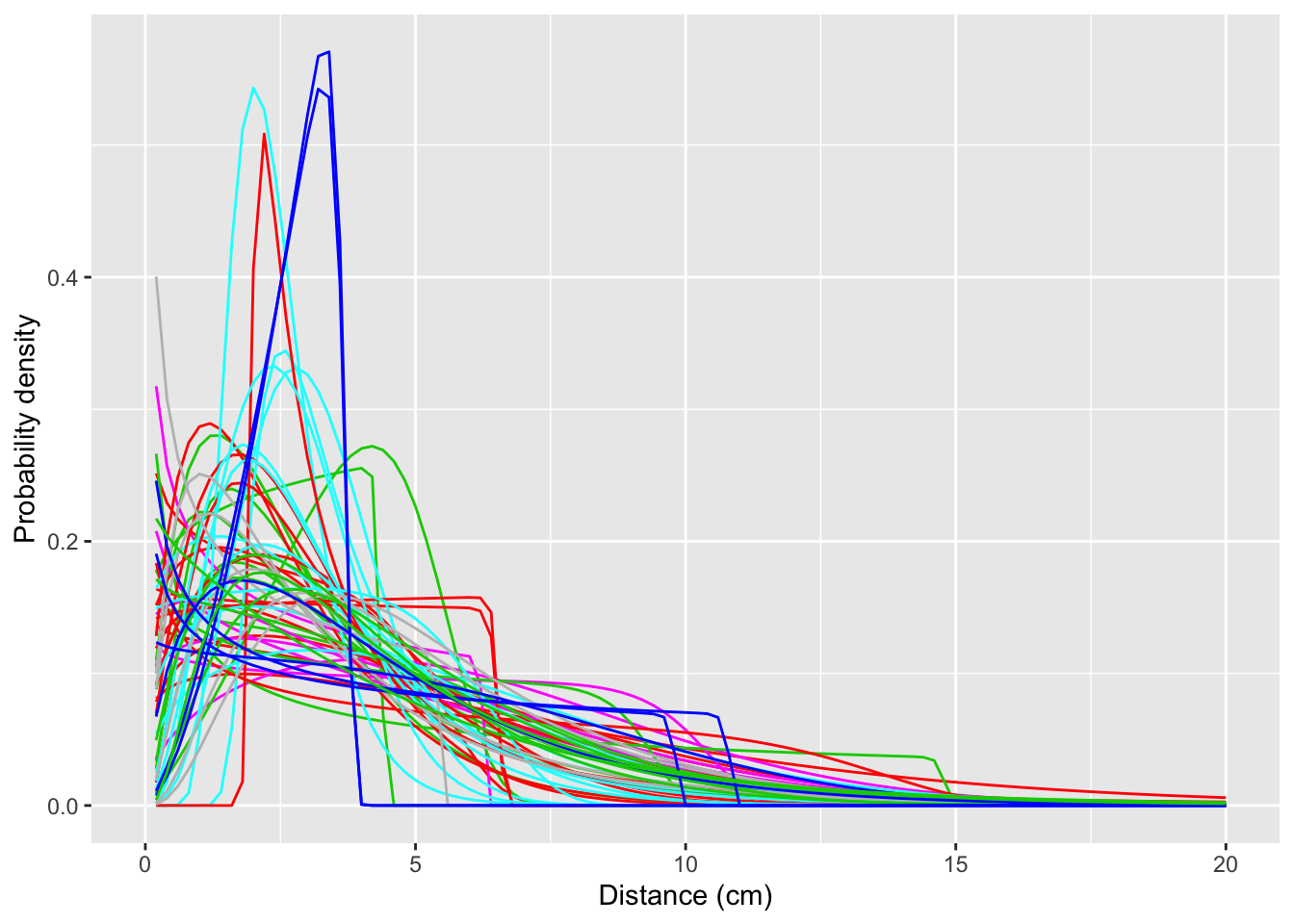
There are a lot of strongly squared-off distributions, which reflect datsets that have nearly uniform distance distributions.
Let’s look at the scatter of parameters:
names(fiteachgg)[5:7] <- c("mu", "sigma", "Q")
library(GGally)
ggpairs(fiteachgg, aes(color = RIL), columns = 5:7)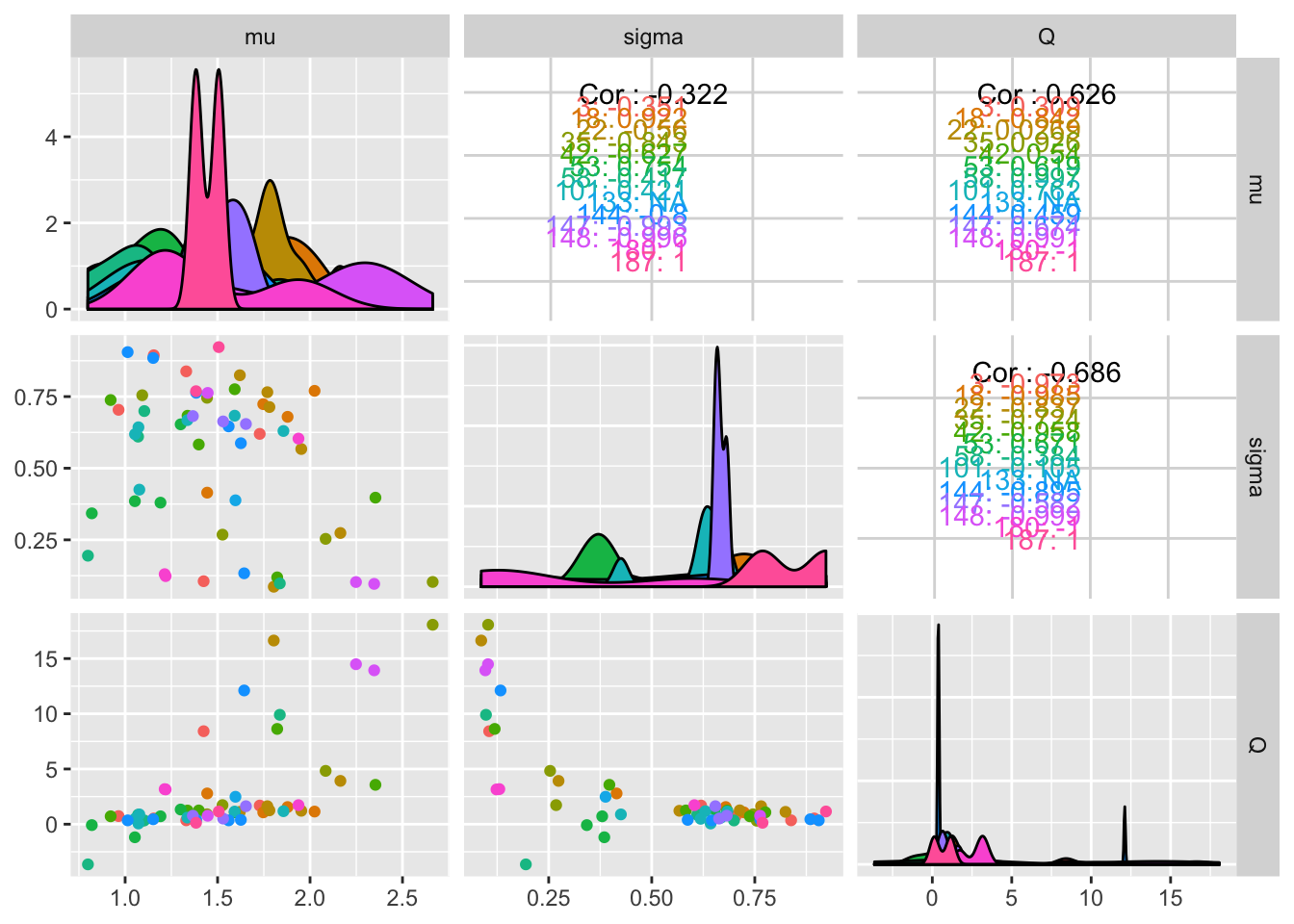
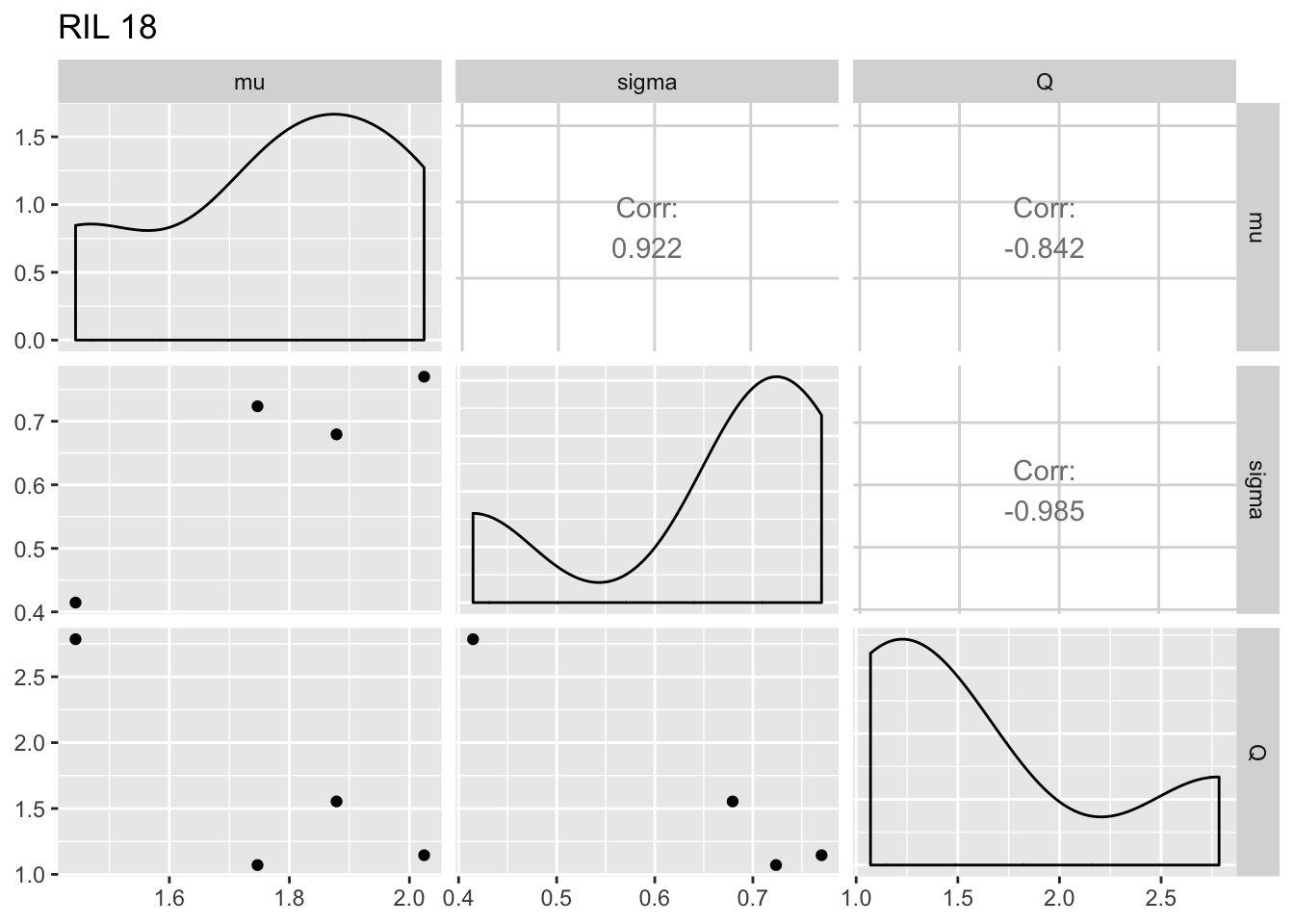
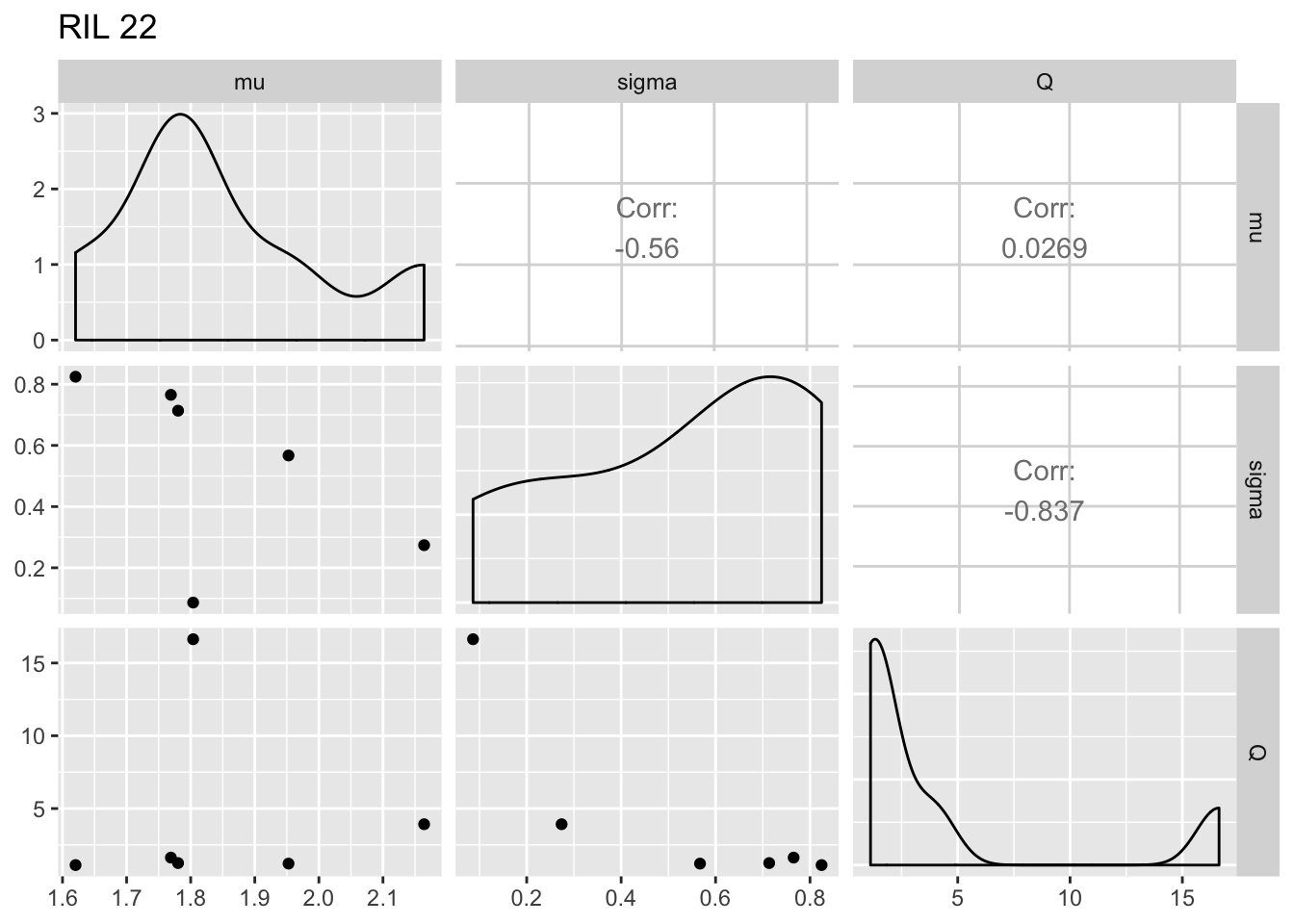
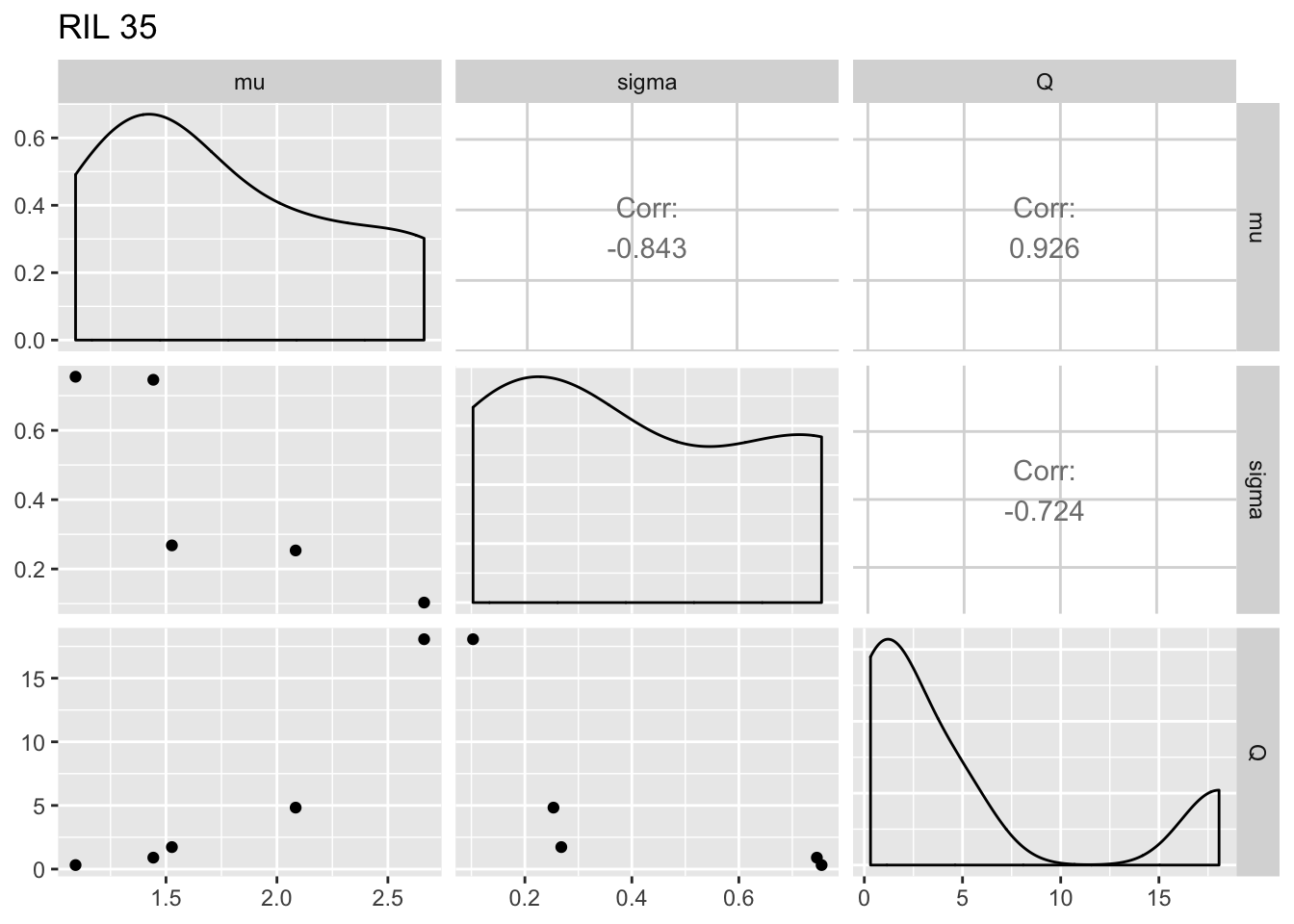
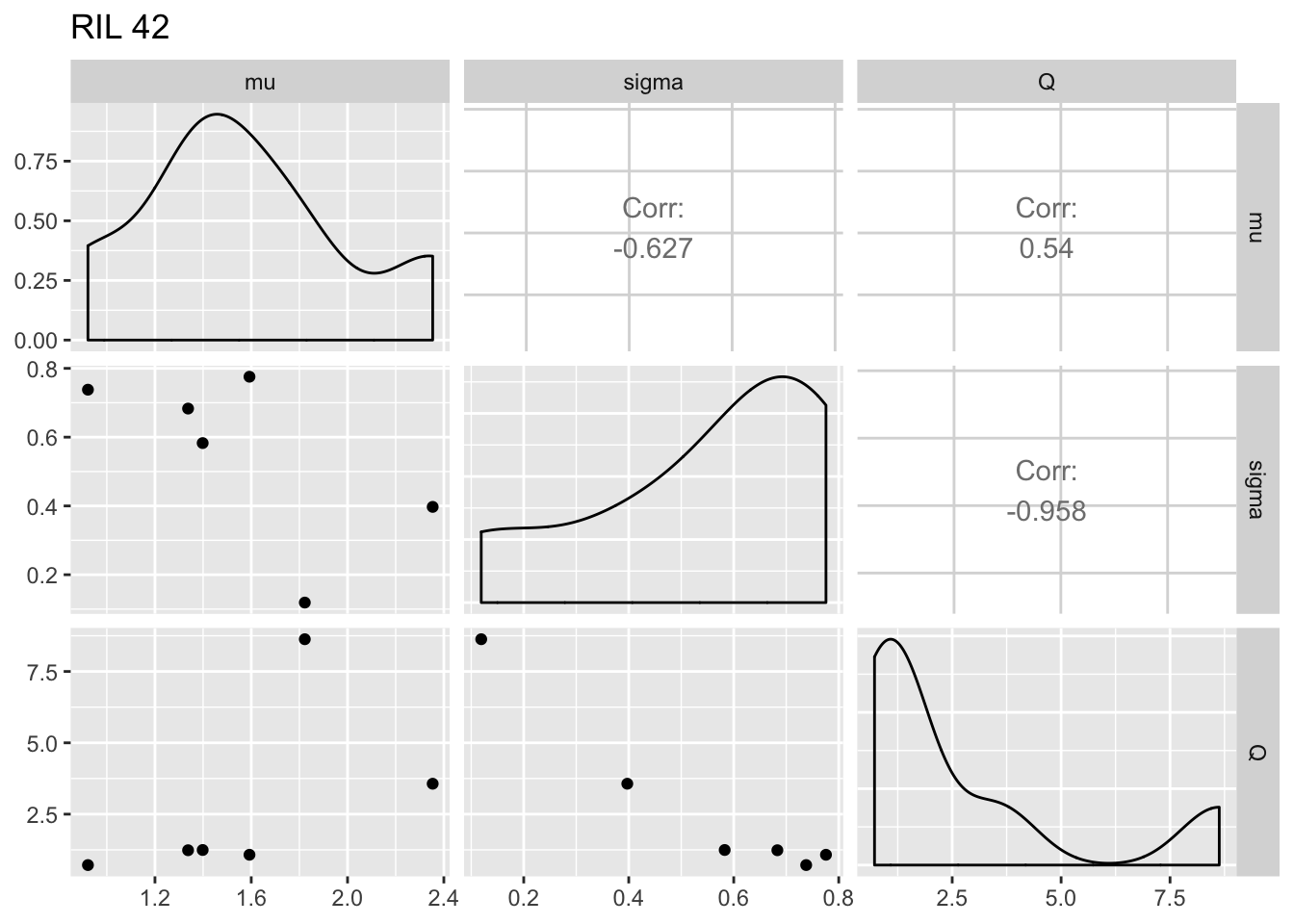
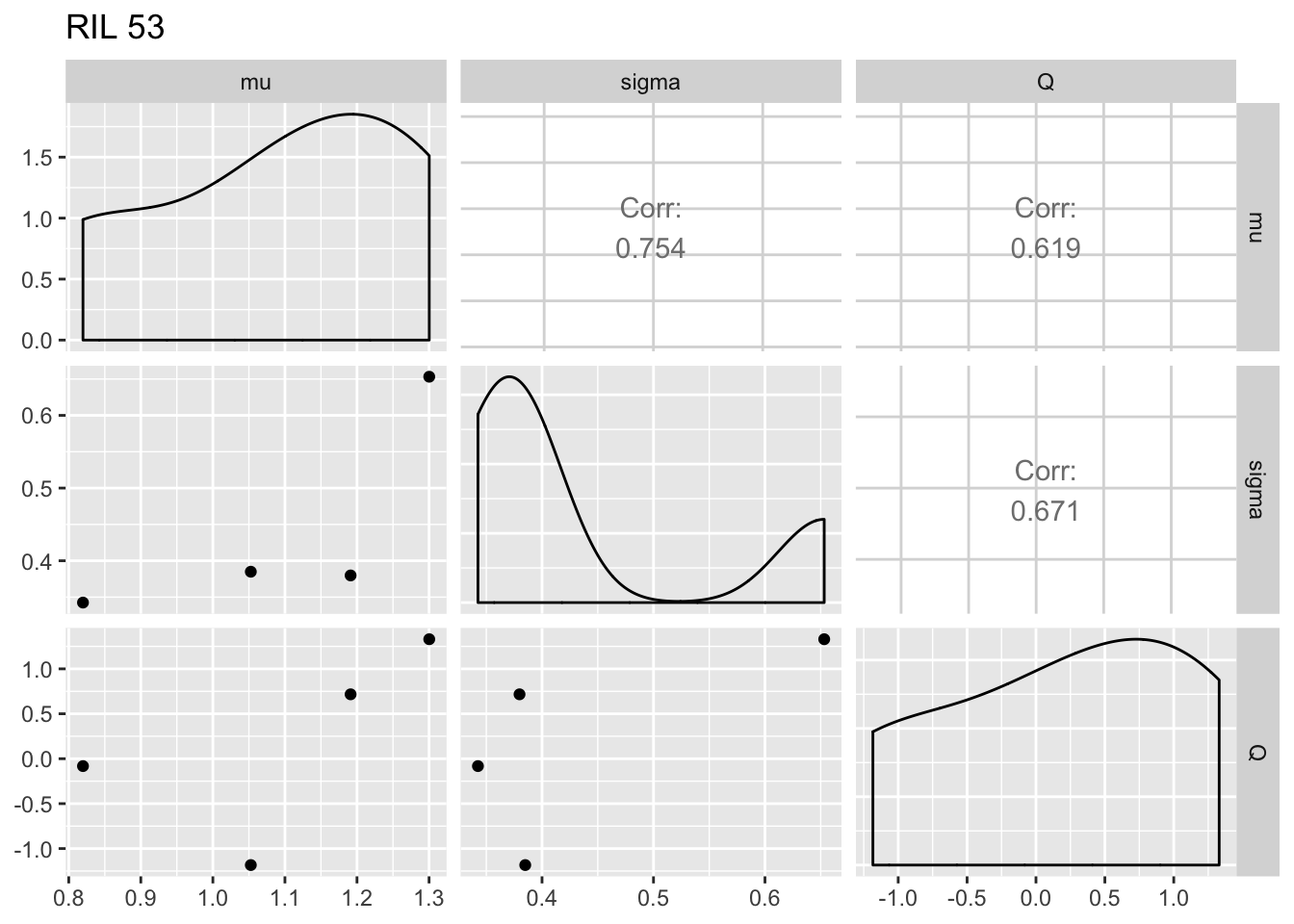
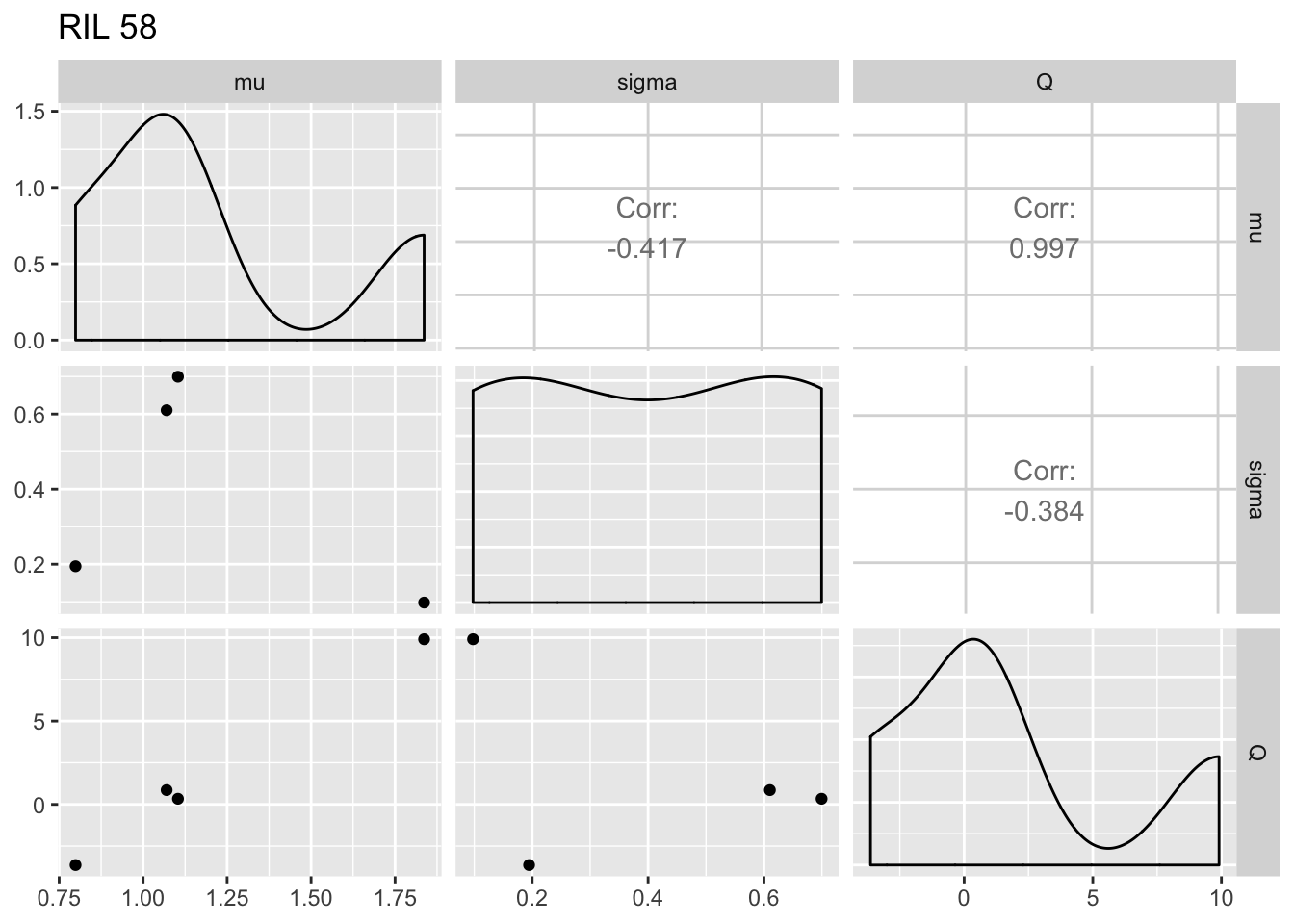
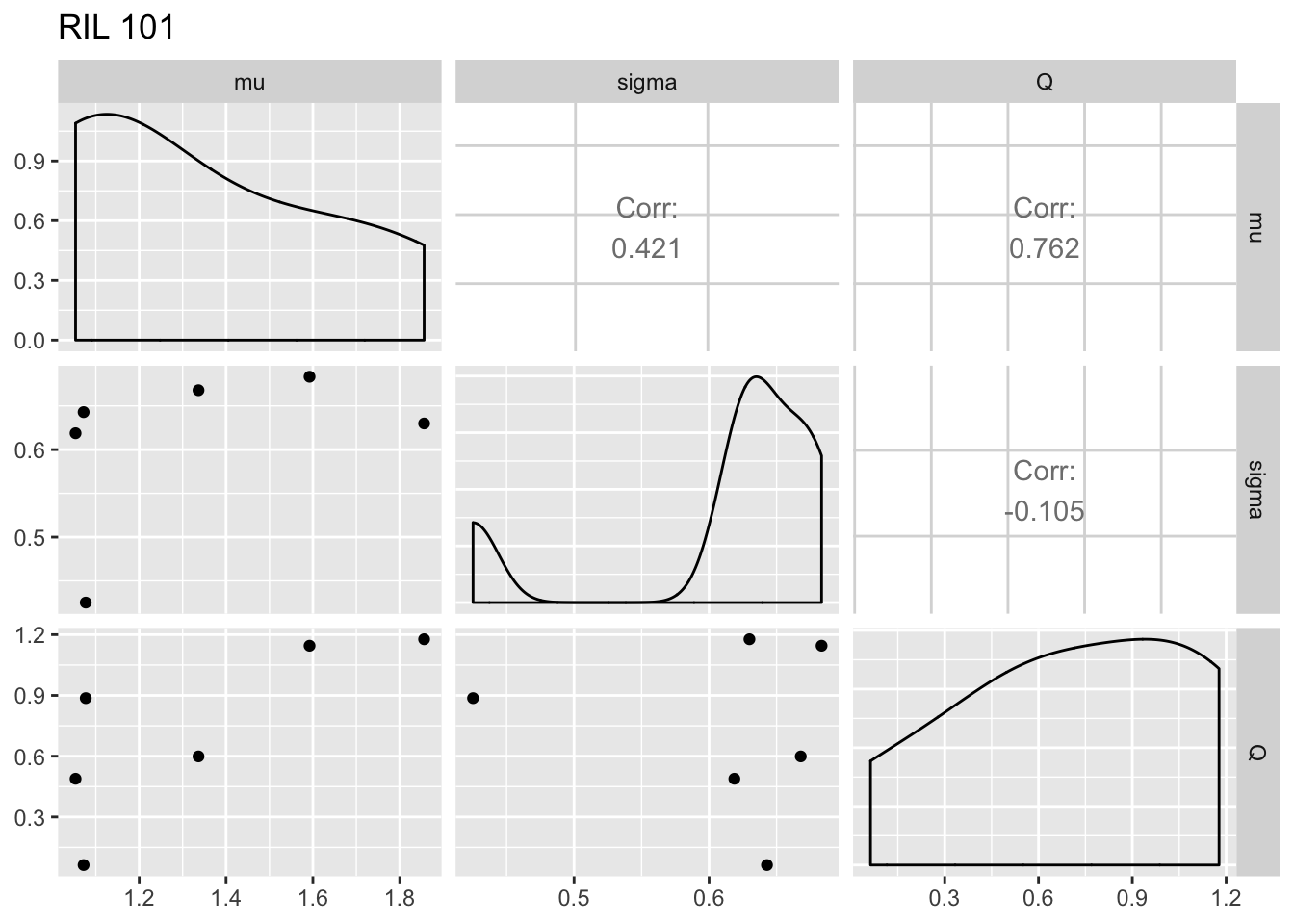
It’s somewhat hard to see from this what the within-RIL patterns look like. Make plots by RIL:
for (i in RIL_list) {
fegg <- filter(fiteachgg, RIL == i)
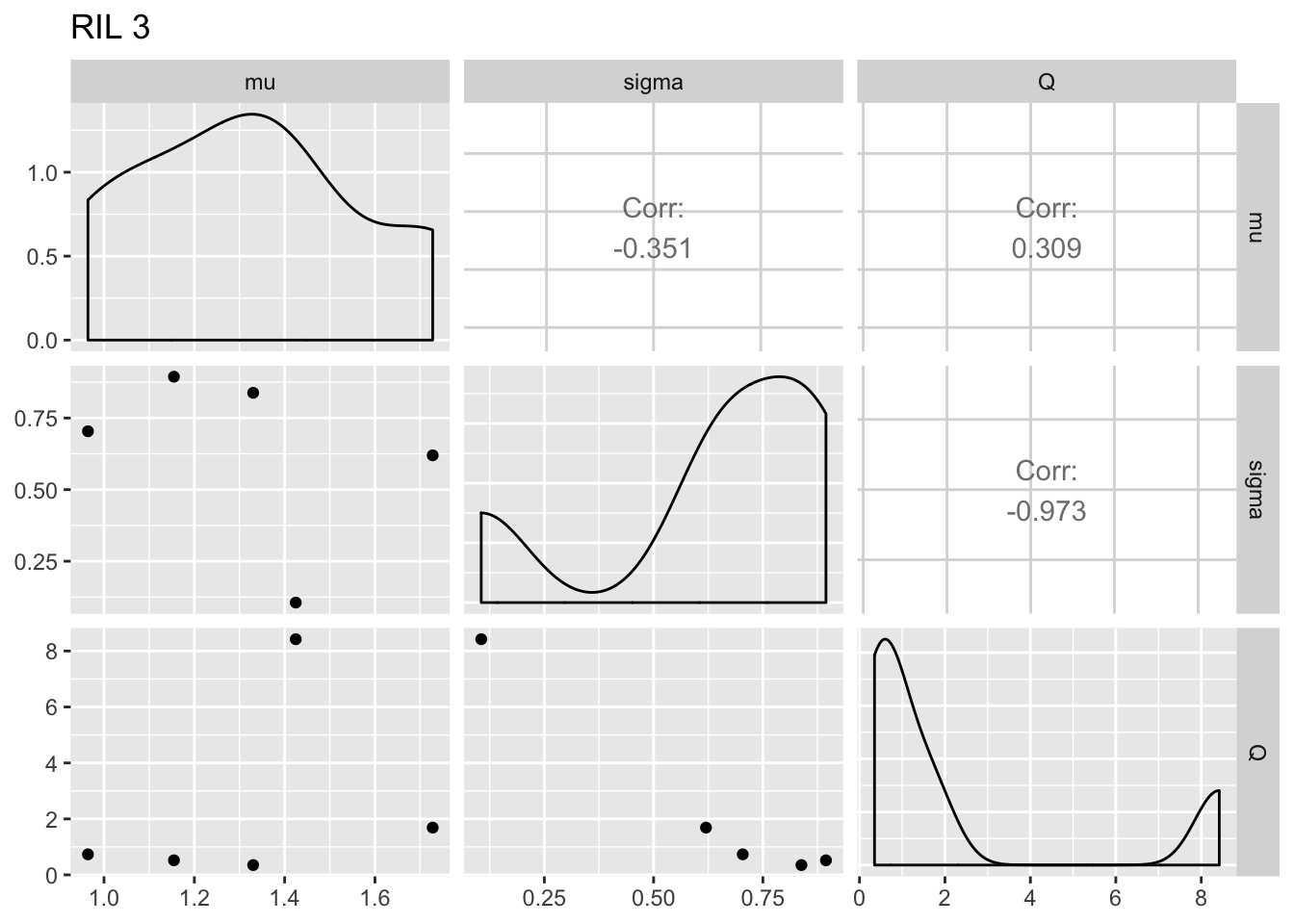
print(ggpairs(fegg, columns = 5:7) + ggtitle(paste("RIL", i)))
}
Warning: Groups with fewer than two data points have been dropped.
Warning: Groups with fewer than two data points have been dropped.
Warning: Groups with fewer than two data points have been dropped.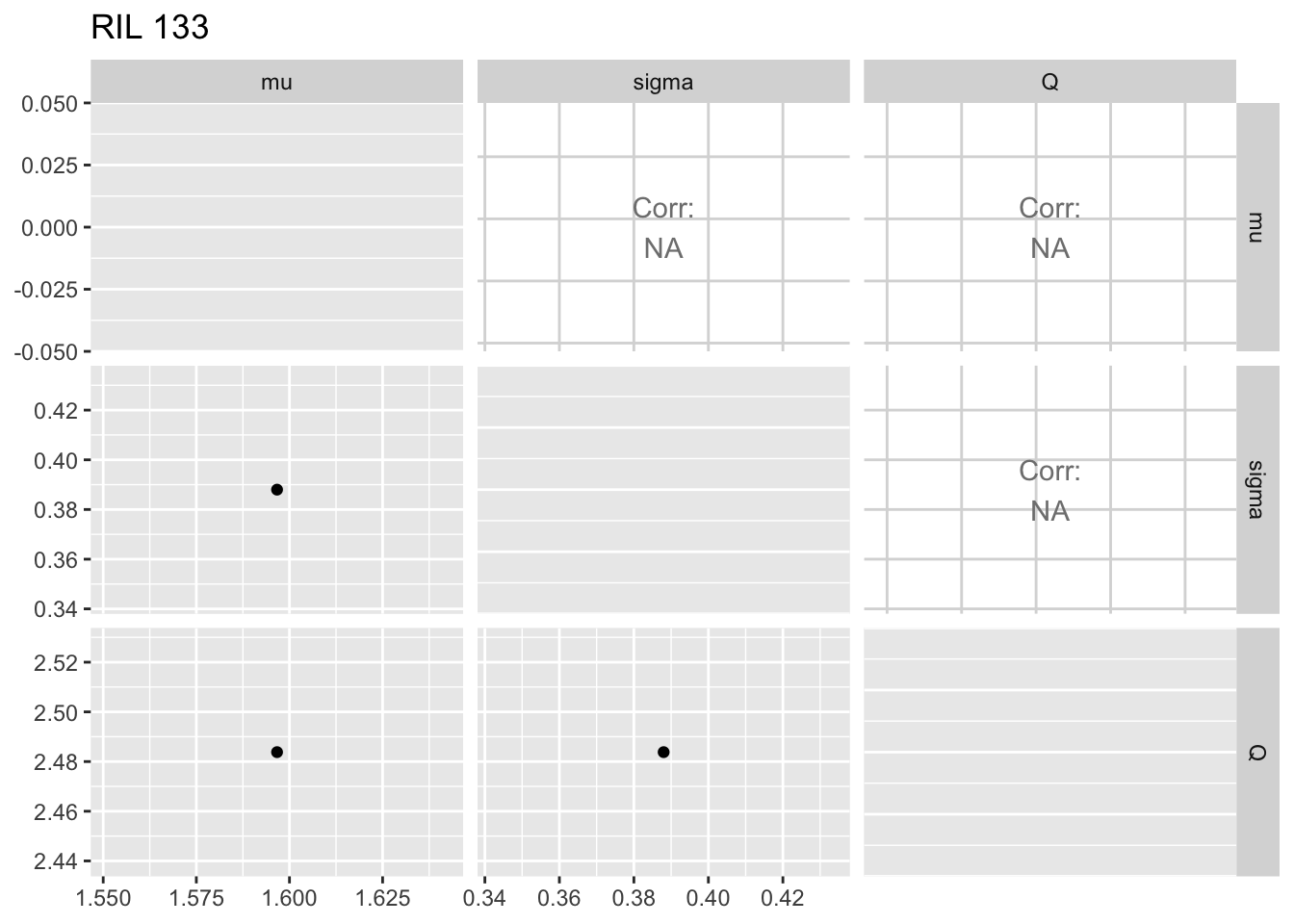
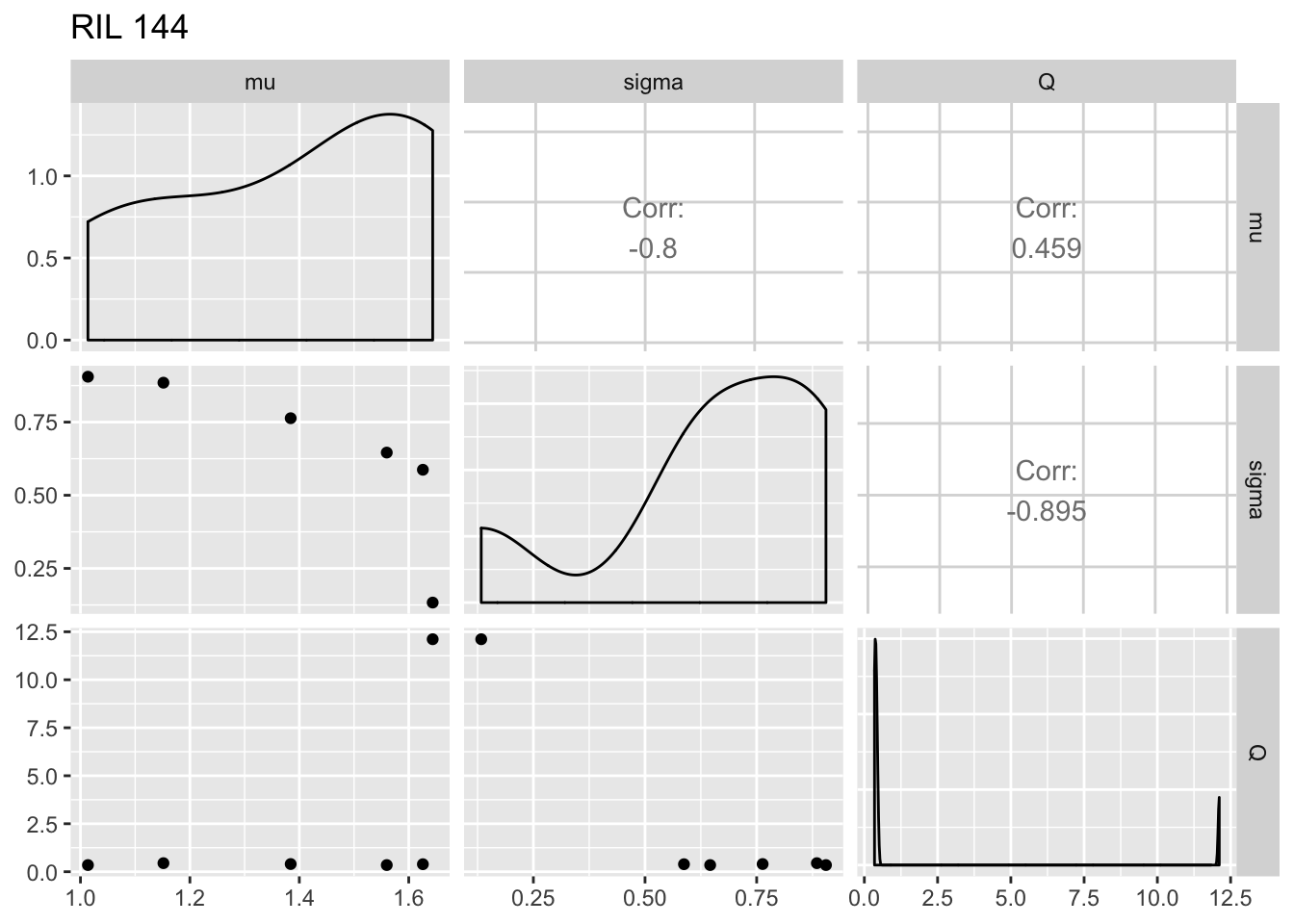
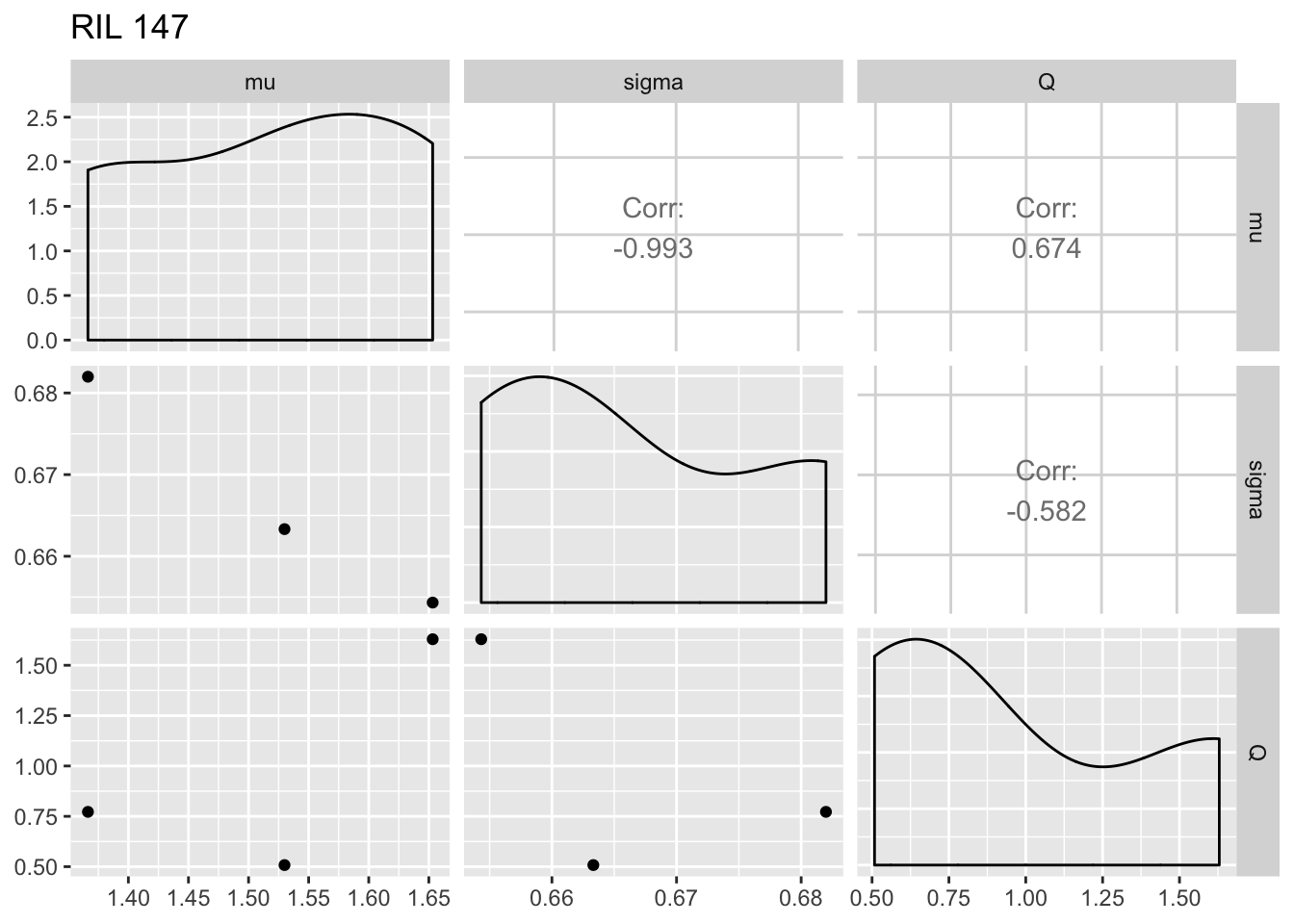
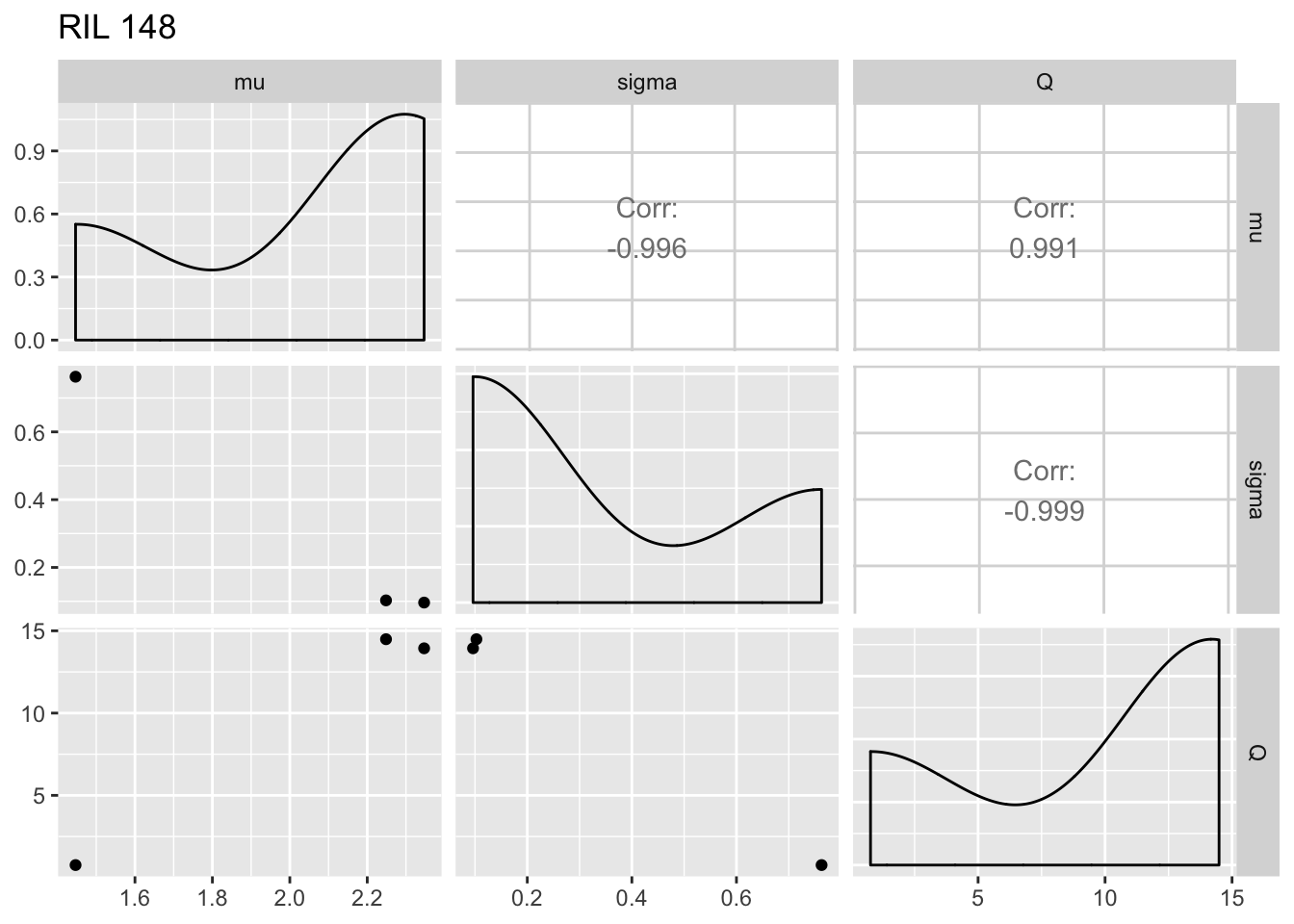
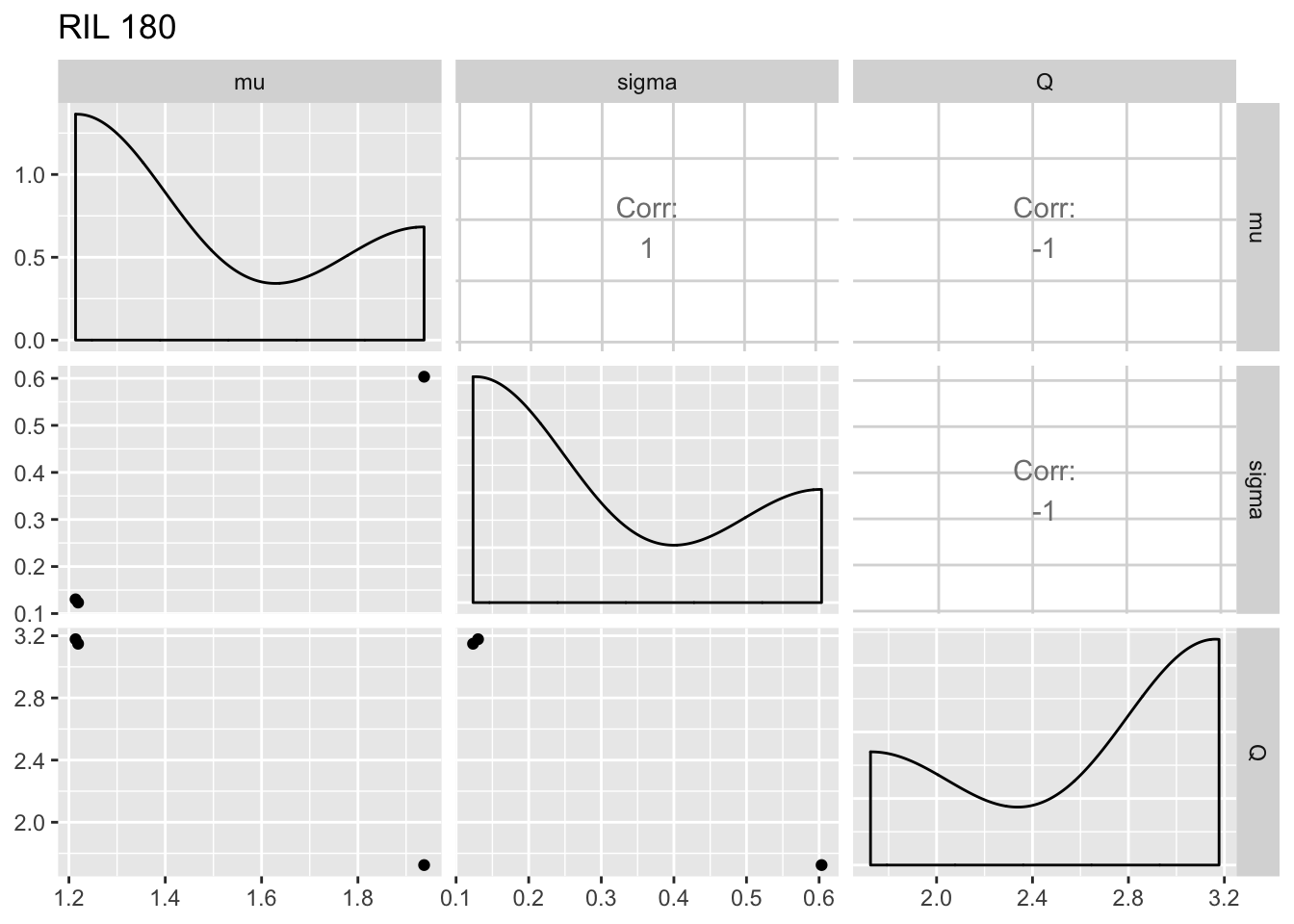
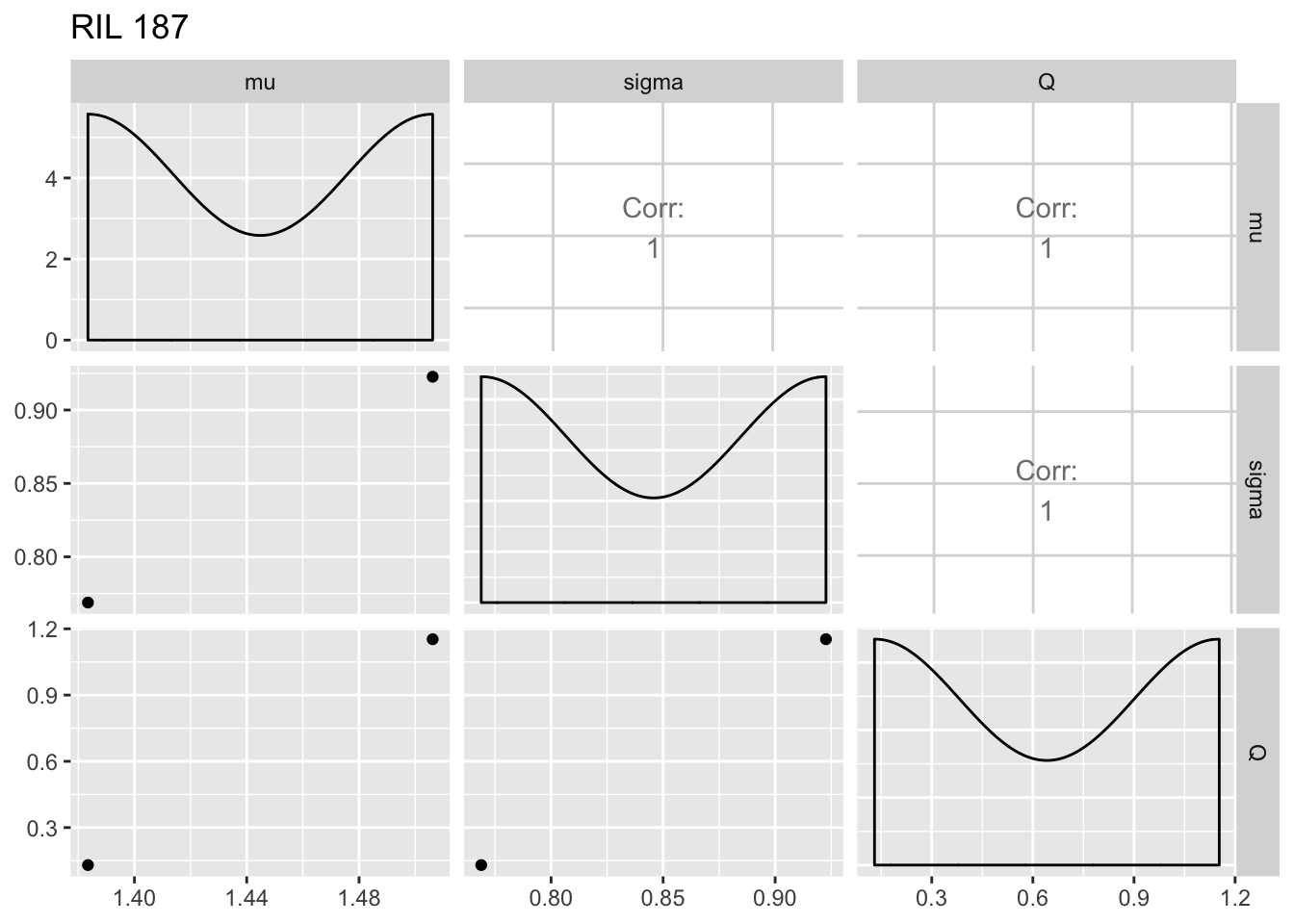
The within-RIL patterns seem reasonable, except for the fact that occasional large values of \(Q\) seem like outliers.
Let’s see if there’s evidence that the parameters vary across RIL:
summary(aov(cbind(mu, sigma, Q) ~ RIL, data = fiteachgg)) Response mu :
Df Sum Sq Mean Sq F value Pr(>F)
RIL 13 3.6180 0.27830 2.076 0.03599 *
Residuals 44 5.8984 0.13406
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Response sigma :
Df Sum Sq Mean Sq F value Pr(>F)
RIL 13 0.97667 0.075128 1.1694 0.3324
Residuals 44 2.82676 0.064245
Response Q :
Df Sum Sq Mean Sq F value Pr(>F)
RIL 13 268.63 20.664 1.0762 0.4031
Residuals 44 844.86 19.201 It looks like there’s clear evidence for genotypic heterogeneity only in the mean dispersal distance, although there is a lot of non-normality in the other parameters. However, I don’t see an easy way to maintain the correlations when only having one of the parameters vary by RIL.
Continuing November 15
The last question involves checking that within-genotype heterogeneity exists by comparing AIC. First calculate summed AICs:
AIC_sums <- group_by(fiteachgg, RIL) %>%
summarize(AIC_sum = sum(AIC))And now calculate the AICs of the homogeneous models for each RIL:
RIL_list <- levels(disperseRILgood$RIL)
fitall <- NULL
for (i in RIL_list) {
disperseRILi <- filter(disperseRILgood, RIL == i)
fitalli <- cbind(RIL = i,
fit_dispersal_untruncated(disperseRILi,
model = "gengamma",
control=controls))
fitall <- rbind(fitall, fitalli)
}This fails for RIL 187. Also, this has me looking back, and realizing that a number of replicates are failing also. These are: 19 (RIL 22), 40 (RIL 53), 77 (RIL 187).
And finally, the Delta-AICs:
fitall RIL ID model AIC par1 par2 par3 se1
1 3 2 hnorm 1511.9310 5.0388899 NA NA 0.199209492
2 3 2 exp 1516.6611 0.2594586 NA NA 0.014499437
3 3 2 lnorm 1505.2379 1.0276544 0.8514891 NA 0.048624634
4 3 2 gamma 1495.7228 1.5072419 0.3894532 NA 0.122773151
5 3 2 weibull 1498.3596 1.2415999 4.1520121 NA 0.056221877
6 3 2 invgauss 1508.6467 3.8869020 4.1370553 NA 0.210528093
7 3 2 logis 1634.2779 3.4155826 1.6533859 NA 0.158958051
8 3 2 invgamma 1541.9803 1.6991632 3.5043180 NA 0.134799747
9 3 2 gengamma 1496.9185 1.2839538 0.8321763 0.6453733 0.090725695
10 18 7 hnorm 2333.6060 6.6789297 NA NA 0.224548260
11 18 7 exp 2355.7947 0.1922181 NA NA 0.009136068
12 18 7 lnorm 2374.3679 1.3004987 0.9157878 NA 0.044198089
13 18 7 gamma 2332.6055 1.4266885 0.2735565 NA 0.096661627
14 18 7 weibull 2330.2654 1.2427466 5.5864781 NA 0.048678447
15 18 7 invgauss 2391.1772 5.2315842 4.6249246 NA 0.264340530
16 18 7 logis 2511.0077 4.6988302 2.2612716 NA 0.187144427
17 18 7 invgamma 2459.7309 1.4031563 3.5266794 NA 0.092275176
18 18 7 gengamma 2331.9320 1.7564780 0.7916559 1.0922657 0.073903876
19 22 11 hnorm 3733.2116 5.9938671 NA NA 0.156058920
20 22 11 exp 3806.2926 0.2090507 NA NA 0.007693484
21 22 11 lnorm 3850.5887 1.2327422 0.9071497 NA 0.033974359
22 22 11 gamma 3759.2482 1.4789190 0.3082259 NA 0.078783078
23 22 11 weibull 3747.2270 1.2956221 5.1781480 NA 0.040384322
24 22 11 invgauss 3877.5407 4.8155760 4.4300435 NA 0.184692991
25 22 11 logis 4004.9548 4.4442943 2.0254378 NA 0.131008951
26 22 11 invgamma 3999.9828 1.4188416 3.3525712 NA 0.072809866
27 22 11 gengamma 3737.0166 1.8118035 0.6938882 1.4708484 0.054394784
28 35 17 hnorm 1232.5902 4.9688465 NA NA 0.216969870
29 35 17 exp 1248.8923 0.2569719 NA NA 0.015858835
30 35 17 lnorm 1236.4992 1.0525098 0.8347940 NA 0.052562961
31 35 17 gamma 1226.2962 1.5978068 0.4087968 NA 0.142629779
32 35 17 weibull 1227.5179 1.2976015 4.2327076 NA 0.065431204
33 35 17 invgauss 1237.8219 3.9228724 4.3959124 NA 0.228760695
34 35 17 logis 1331.3071 3.5089799 1.6438121 NA 0.175949227
35 35 17 invgamma 1266.3845 1.7356859 3.6868791 NA 0.151135881
36 35 17 gengamma 1228.2540 1.3448097 0.7967839 0.7450910 0.101756463
37 42 23 hnorm 1650.3890 4.8603826 NA NA 0.182535406
38 42 23 exp 1673.9162 0.2621699 NA NA 0.013915069
39 42 23 lnorm 1676.2911 1.0311094 0.8533783 NA 0.046345635
40 42 23 gamma 1648.1848 1.5499922 0.4043940 NA 0.122193040
41 42 23 weibull 1646.7659 1.2902572 4.1384836 NA 0.056955699
42 42 23 invgauss 1684.5425 3.8513298 4.1314755 NA 0.197357137
43 42 23 logis 1771.5264 3.4738297 1.5782805 NA 0.144942641
44 42 23 invgamma 1731.7145 1.6504403 3.3871958 NA 0.125410463
45 42 23 gengamma 1648.7631 1.4239303 0.7738406 1.0097373 0.078255926
46 53 29 hnorm 429.7140 4.0109363 NA NA 0.283664161
47 53 29 exp 445.7333 0.3033483 NA NA 0.030299816
48 53 29 lnorm 408.9090 1.0108638 0.6220451 NA 0.063402770
49 53 29 gamma 411.5572 2.6410337 0.7951563 NA 0.380087899
50 53 29 weibull 418.3143 1.5895875 3.7137872 NA 0.118361188
51 53 29 invgauss 410.2606 3.3243375 7.1932315 NA 0.226660150
52 53 29 logis 435.4756 3.0231119 1.0915003 NA 0.186683643
53 53 29 invgamma 415.6794 2.9022171 6.6836030 NA 0.417864121
54 53 29 gengamma 410.5883 1.0575866 0.6246299 0.1559369 0.103877895
55 58 35 hnorm 531.7684 5.1431927 NA NA 0.344724519
56 58 35 exp 538.9394 0.2479601 NA NA 0.023489710
57 58 35 lnorm 521.5722 1.1197090 0.7666892 NA 0.073795836
58 58 35 gamma 523.7217 1.8160605 0.4483629 NA 0.242670008
59 58 35 weibull 526.8304 1.3516444 4.4329575 NA 0.100116673
60 58 35 invgauss 521.5568 4.0574941 5.4566599 NA 0.331633115
61 58 35 logis 570.7780 3.5570290 1.6435988 NA 0.267330913
62 58 35 invgamma 529.6351 2.0272887 4.8041333 NA 0.269249244
63 58 35 gengamma 523.0619 1.2033558 0.7695860 0.2284970 0.139012867
64 101 41 hnorm 846.3974 4.9148453 NA NA 0.258495256
65 101 41 exp 870.6626 0.2506195 NA NA 0.018625511
66 101 41 lnorm 834.2066 1.1427009 0.7285090 NA 0.054989649
67 101 41 gamma 832.3067 2.0695729 0.5162091 NA 0.217052829
68 101 41 weibull 836.2746 1.4763924 4.4441124 NA 0.086317452
69 101 41 invgauss 834.0688 4.0143890 6.1290169 NA 0.241726702
70 101 41 logis 893.0266 3.6632398 1.5441352 NA 0.200788748
71 101 41 invgamma 850.2491 2.1554531 5.3026654 NA 0.224804026
72 101 41 gengamma 833.2313 1.2971754 0.7166021 0.4397894 0.103525397
73 133 48 hnorm 227.3942 3.7444630 NA NA 0.359146494
74 133 48 exp 240.4369 0.3123745 NA NA 0.042291594
75 133 48 lnorm 238.3123 0.9508513 0.7369799 NA 0.102237162
76 133 48 gamma 230.5174 2.1818207 0.6752890 NA 0.449849244
77 133 48 weibull 227.1801 1.6919449 3.6041470 NA 0.203989299
78 133 48 invgauss 239.3137 3.2423931 5.0089310 NA 0.353784297
79 133 48 logis 235.6373 3.1896442 1.1317759 NA 0.274186003
80 133 48 invgamma 248.1875 2.0203038 4.0546765 NA 0.397839381
81 133 48 gengamma 223.4773 1.5966659 0.3879888 2.4837918 0.146482986
82 144 53 hnorm 1204.0331 5.3485299 NA NA 0.239888389
83 144 53 exp 1213.5484 0.2415531 NA NA 0.015314065
84 144 53 lnorm 1205.8245 1.1093938 0.8442704 NA 0.054544499
85 144 53 gamma 1193.9392 1.5698795 0.3776837 NA 0.144015345
86 144 53 weibull 1195.5957 1.2763988 4.4862028 NA 0.065181301
87 144 53 invgauss 1210.8620 4.1714023 4.5078361 NA 0.254381227
88 144 53 logis 1288.6114 3.7093417 1.7141996 NA 0.186523083
89 144 53 invgamma 1240.7865 1.6737447 3.7196990 NA 0.149682377
90 144 53 gengamma 1195.8324 1.3986804 0.8058457 0.7337897 0.094695262
91 147 59 hnorm 646.0046 5.2482816 NA NA 0.320365329
92 147 59 exp 664.7475 0.2340221 NA NA 0.020187036
93 147 59 lnorm 654.1668 1.2015062 0.7694050 NA 0.067379380
94 147 59 gamma 642.8273 1.9386609 0.4514709 NA 0.241916272
95 147 59 weibull 642.5806 1.4569785 4.7361525 NA 0.100909016
96 147 59 invgauss 659.1130 4.3046261 5.7683683 NA 0.320994354
97 147 59 logis 675.1196 3.9445190 1.5880402 NA 0.236002298
98 147 59 invgamma 678.5389 1.8621007 4.6784011 NA 0.226884768
99 147 59 gengamma 644.3591 1.5160773 0.6968445 0.8841672 0.104655976
100 148 66 hnorm 229.8761 5.1881238 NA NA 0.531149625
101 148 66 exp 234.2882 0.2423849 NA NA 0.035070346
102 148 66 lnorm 237.2551 1.0745790 0.9050554 NA 0.133702590
103 148 66 gamma 233.3937 1.4492002 0.3500727 NA 0.302127832
104 148 66 weibull 232.8347 1.2754371 4.4581887 NA 0.158123287
105 148 66 invgauss 236.9562 4.1548651 3.9100832 NA 0.619413502
106 148 66 logis 252.2158 3.8868109 1.8353380 NA 0.473632006
107 148 66 invgamma 243.2677 1.5028643 3.0994517 NA 0.302706843
108 148 66 gengamma 233.3121 1.8416956 0.5849284 2.0543650 0.243003310
109 180 73 hnorm 377.5094 4.9059108 NA NA 0.386776470
110 180 73 exp 385.8780 0.2548929 NA NA 0.028397729
111 180 73 lnorm 369.3690 1.1261760 0.7186963 NA 0.081338494
112 180 73 gamma 370.4325 2.0546154 0.5211240 NA 0.324408632
113 180 73 weibull 373.3110 1.4368411 4.3582895 NA 0.123713158
114 180 73 invgauss 370.0386 3.9481418 6.1598001 NA 0.352533002
115 180 73 logis 399.3398 3.4943001 1.4964986 NA 0.285621350
116 180 73 invgamma 376.0510 2.2369659 5.4692145 NA 0.351941770
117 180 73 gengamma 370.7943 1.2168384 0.7196190 0.2632830 0.144647536
118 187 77 hnorm 600.1028 5.6076359 NA NA 0.359938804
119 187 77 exp 586.6146 0.2482301 NA NA 0.022531076
120 187 77 lnorm 589.2781 0.9824097 0.9589539 NA 0.089440131
121 187 77 gamma 587.2087 1.1751535 0.2911932 NA 0.156702651
122 187 77 weibull 587.6610 1.0773545 4.1536274 NA 0.080505764
123 187 77 invgauss 590.1878 4.0628152 3.2396337 NA 0.412823524
124 187 77 logis 659.6549 3.4423852 1.9167085 NA 0.297914168
125 187 77 invgamma 602.0482 1.4511312 2.7233176 NA 0.187413487
se2 se3
1 NA NA
2 NA NA
3 0.03787923 NA
4 0.03605905 NA
5 0.19893631 NA
6 0.37446416 NA
7 0.07905673 NA
8 0.34265431 NA
9 0.03915315 0.1931778
10 NA NA
11 NA NA
12 0.03415210 NA
13 0.02138685 NA
14 0.22645156 NA
15 0.34965191 NA
16 0.09039535 NA
17 0.29397773 NA
18 0.03863082 0.1600487
19 NA NA
20 NA NA
21 0.02647815 NA
22 0.01877326 NA
23 0.15582283 NA
24 0.26245562 NA
25 0.06195241 NA
26 0.21875564 NA
27 0.03141013 0.1413330
28 NA NA
29 NA NA
30 0.04056515 NA
31 0.04129192 NA
32 0.21414235 NA
33 0.43461236 NA
34 0.08598265 NA
35 0.39271573 NA
36 0.04476098 0.2259475
37 NA NA
38 NA NA
39 0.03661533 NA
40 0.03594411 NA
41 0.18103817 NA
42 0.36051209 NA
43 0.07100910 NA
44 0.32041292 NA
45 0.03912709 0.1752844
46 NA NA
47 NA NA
48 0.04758629 NA
49 0.12363068 NA
50 0.24889581 NA
51 1.11826075 NA
52 0.09449311 NA
53 1.08788976 NA
54 0.04764835 0.2741321
55 NA NA
56 NA NA
57 0.05552359 NA
58 0.06730990 NA
59 0.33063498 NA
60 0.80278721 NA
61 0.13425474 NA
62 0.75327986 NA
63 0.05545398 0.3195632
64 NA NA
65 NA NA
66 0.04114385 NA
67 0.06002106 NA
68 0.23781343 NA
69 0.70368055 NA
70 0.09659667 NA
71 0.64671380 NA
72 0.04247629 0.2507150
73 NA NA
74 NA NA
75 0.08070351 NA
76 0.15098109 NA
77 0.30628742 NA
78 1.11658392 NA
79 0.12652023 NA
80 0.96008649 NA
81 0.10160358 0.8935616
82 NA NA
83 NA NA
84 0.04226313 NA
85 0.03930260 NA
86 0.23683991 NA
87 0.45837812 NA
88 0.09260701 NA
89 0.40933298 NA
90 0.04381884 0.2015349
91 NA NA
92 NA NA
93 0.05172700 NA
94 0.06254573 NA
95 0.29741663 NA
96 0.78611460 NA
97 0.11680141 NA
98 0.68359058 NA
99 0.05308470 0.2459879
100 NA NA
101 NA NA
102 0.10334502 NA
103 0.08364166 NA
104 0.53729192 NA
105 0.90926721 NA
106 0.21665714 NA
107 0.78619453 NA
108 0.15725998 0.8707995
109 NA NA
110 NA NA
111 0.06110918 NA
112 0.09119871 NA
113 0.35962614 NA
114 1.06339788 NA
115 0.14484199 NA
116 1.00102367 NA
117 0.06086707 0.3455521
118 NA NA
119 NA NA
120 0.07103567 NA
121 0.04546050 NA
122 0.37335151 NA
123 0.48932825 NA
124 0.14881017 NA
125 0.45250513 NAfitall$AIC - AIC_sums$AIC_sumWarning in fitall$AIC - AIC_sums$AIC_sum: longer object length is not a
multiple of shorter object length [1] 26.102510 -787.210018 -2188.243463 374.245551 -126.753103
[6] 1112.943299 1209.835815 703.683879 1273.441164 1152.147602
[11] 1706.944326 2134.731899 2004.630143 1840.765835 905.348663
[16] 207.136587 -1233.750518 1210.454729 2108.098905 3410.589206
[21] 3426.146583 2920.951772 3523.749602 2696.082287 3356.104465
[26] 3760.346761 3409.041274 743.090650 -236.936186 -1067.371900
[31] -2467.185177 106.040674 -387.290793 935.603740 841.942454
[36] 389.957497 1426.911669 492.457737 1027.440708 1408.548776
[41] 1318.790626 1195.042931 285.697927 -572.156630 -2044.718325
[46] -691.763283 -1179.379462 13.205586 -12.884900 -419.982174
[51] 186.783207 -745.982818 -233.170912 170.952300 203.793054
[56] 49.439864 -964.256335 -1780.149417 -3166.650972 -599.920459
[61] -1054.334691 133.931676 98.619804 8.100961 647.185270
[66] -347.251799 183.456348 596.638601 506.093495 403.527047
[71] -635.579387 -1470.639872 -3466.087189 -881.040389 -1386.800474
[76] -165.185991 -197.262025 -598.982814 12.160000 -933.270869
[81] -425.373010 964.397015 885.573120 716.325003 -291.889275
[86] -1108.275454 -2482.619401 167.134149 -384.326188 800.129017
[91] 221.562533 -173.548970 430.689459 -538.631067 -6.269723
[96] 419.476925 347.144292 189.039357 -841.469386 -2073.995021
[101] -3459.193154 -884.222130 -1391.719044 -162.868690 -187.485860
[106] -586.080620 19.790374 -948.146335 -271.340935 146.241921
[111] 41.393658 -119.067049 -1112.517524 -1933.832532 -3294.141575
[116] -745.426225 -1254.318462 204.399456 162.172516 -249.018412
[121] 363.731397 -593.797453 -58.662595 420.018877 274.072874